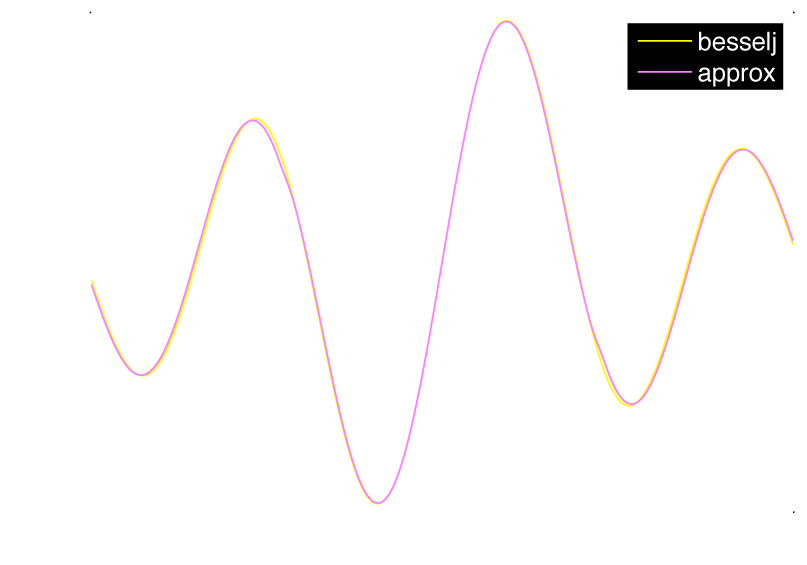
With the help of Michael Croucher of the walkingrandomly weblog, who graciously spent some time optimising one of the slowest components of the Matlab code, we were able to come up with an approximation to the Bessel function which was about two times faster than Matlab’s internal function. However, then I had to smoothen out the crossover point using error functions, and now it has lost some of the speed it had gained in favour of smoothness. It is now about 40% faster than Matlab’s Bessel function, when approximated using only 5 polynomial terms.

It looks like this, with the crossover gradient centre at 4.5:

So there remains a small discrepancy for such low polynomial numbers, but it should be possible to obtain a good speed increase with this in cylinder and disk scattering functions. Please grab yourself a copy of the code, and I’ll be happy (albeit perhaps slow in the coming two weeks) to include more improvements!

bessel_li_gross

p.s.: I forgot to mention how to compile the code for your computer. At this point, there’s a compiled version available for intel Macs. If you do not have that one, but you do have the matlab (”mex”) compiler, I suggest you follow the following steps:

1. make sure your mex compiler can find the following include files: mex.h, math.h, omp.h (in my case, I copied a suitable version of omp.h into the bessel_li_gross directory

2. go to the bessel_li_gross directory and type “mex blg_component.c”, or if your compiler complains about not being able to find the omp.h file that you just put in the directory: “mex -I./ blg_component.c” (adds the current path to the search path for files under unix)

3. Play. You can also send me your .mex file so I can add it to the package.