Fancy background subtraction: a second look.

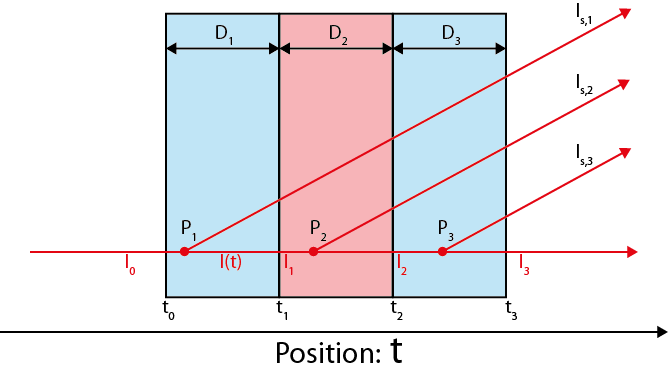
During last week’s visit to BAM in Berlin, I and Ingo played around with some equations. In particular, we were curious if we need to do something special to get the scattering from a sample in a capillary, i.e. a sample between an upstream and a downstream sample cell wall. Long story short: we arrive at a rather ordinary equation after a lengthy derivation.

So we derived the method to extract the sample scattering from the total scattering signal for this case. We discussed this topic before in this post where self-absorption (discussed in this post) was considered, but where the derivation was not completely worked out. To make it easier to derive, we neglect the direction-dependent absorption of the scattered signal(s), but a future derivation may include this term (only for flat walls and phases, as the derivation thereof of round capillary-type cross-sections is ridiculously complex).

We consider three separate processes as an incident photon beam travels through a given phase: the attenuation of the incident beam by the material before a scattering event, a probability for scattering of this attenuated beam, and the attenuation of the scattered radiation by the remaining material of the phase. Each incident and scattered beam is further attenuated by the preceding and subsequent phases. We also assume that the scattering event does not significantly reduce the intensity of the remaining unscattered beam.

The derivation is provided in a separate document here, together with most of the text in this post. I cannot promise I did the derivation in the most efficient way, there may be shorter ways of doing it, and it most certainly will have been done before in literature. Apropos, it very much resembles a nice exercise for an exam question or class derivation, for those who are into teaching small-angle scattering.

Despite the rather long intermediate equations in the derivation, the final equation is quite short:

where is the thickness of the sample phase (only), the measured intensity of sample + cell, the measured intensity of the cell, the primary beam flux, and and the transmission factors measured for the sample + cell and cell measurements, respectively.

There are interesting aspects when we use this background subtraction equation in practice. Firstly, we find that it is not necessary to determine the sample cell wall thickness . Secondly, both the sample measurement and the background measurement are normalised to the thickness of the sample phase only. Lastly, it should be noted that this is, of course, only valid if the same sample cell is used for both the background and the sample measurement.

So, nothing shocking here, but it is interesting that it can be derived from more basic considerations.