There has been some good response to last week’s post, indicating that many of you are or have been in the same bind. Our partial solution might be a bit underwhelming: assume*.
Dr. A. Petzold explains in an e-mail where the problem comes from:
Here I’m in charge for two rather old Kratky cameras currently and we’re expanding with a used SAXSess system. Recently we’ve equipped an old instrument with a Mythen strip detector. During my PhD thesis I’ve had a similar problem as you’ve described in your article.
A multilayer-optics for collimation and monochromatization of the primary beam uses the Bragg principle. Hence not only the wanted Cu-Kalpha radiation is passing the optics but also the 2nd order of twice the energy and the third order of triple the energy and so on. Meaning you have a significant amount of high energy radiation leading to beam hardening as you’ve described.
Our biggest issue with the high energy radiation contamination seems to be that we cannot correctly determine the transmission factor of the materials we measure. While we should have done this before, we need to verify that the transmission factor is the only problem we have.
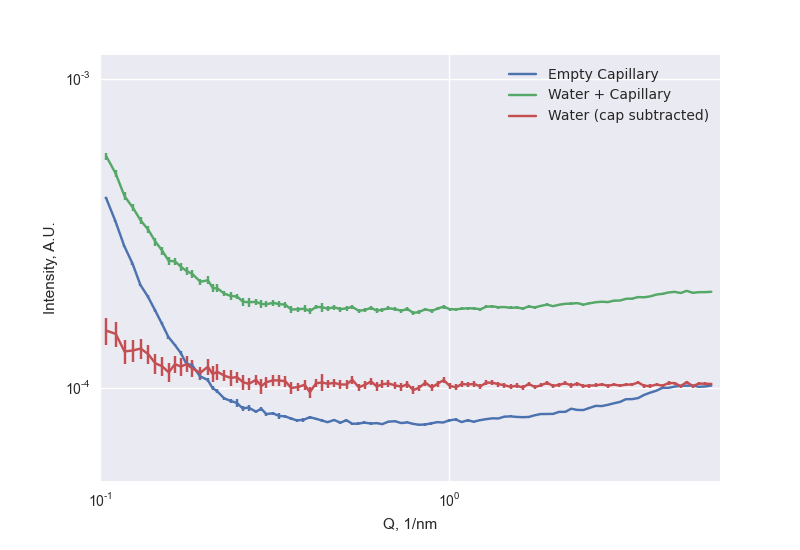
If we follow the right data corrections procedure (including taking transmission factors into account), we should be able to get a good water scattering pattern after subtraction of the capillary scattering. Cue a 30-minute measurement of capillary followed by the same capillary filled with water (easy if you have a flow-through cell). After this, we can subtract the transmission-factor-corrected water scattering pattern from the empty capillary scattering pattern, by assuming the water absorbs with a factor of 0.391). And behold (in Figure 1)! A nice flat scattering profile that underscores two things:
- Our capillary is about 1 mm in diameter at the beam position, and
- The transmission factor is the only issue we have for correct background subtraction.
With this knowledge, we know that by calculating a transmission factor we may get correct data. Since we are usually measuring dilute suspensions in water here, and the capillary is the same for a series of measurements, the assumed transmission factor allows us to continue.
As an added bonus, we see that the background-subtracted water data plateau is at a level of 
A check with a few NIST nanoparticle calibration standards shows that we are actually within 10% of their stated concentrations, which is nice. On the down side, when we play around, we notice that we can get an optically flat plateau even when we vary the assumed transmission factor by up to 20%: the accuracy of this assumption is not the best.
At the moment, we are hunting for better ways to determine our transmission factor. In the SAXSess design, Anton Paar has removed the options for installing a moving slit device, and has removed the revolving beamstop found in the older design (which allowed one to quickly move the beamstop in and out). We still have the option of putting a strong scatterer behind our sample, although that has its own issues as well (as discussed before). A separate, movable detector mounted to the lid may be a viable way forward, and if we make this a fast silicon drift detector, it may be possible to ascertain the spectral purity of the radiation at the same time. Time to put on that hat and the eyepatch and hunt for the booty to pay for it. Yarr!
Or one could go for the solutions put forth by Dr. Petzold:
Usually [the high energy filtering is done] by the detector which uses an lower and upper energy threshold. The Mythen unfortunately only has a lower threshold. In order to get an idea of the problem I’d suggest to perform a threshold scan in the Mythen web interface and plotting the counts of one channel against the threshold (see Fig. 4 in [1]). For us using only Ni-filtered Cu radiation we found approx. 20% of the counts originate from high energy radiation from the bremsstrahlung.
So far I know of 2.5 solutions to your problem:
1. Scan with low threshold (e.g. 6.4keV) and directly afterwards with high threshold (e.g. 9keV) and subtract the measurements channel by channel. This leads to a doubling of the measurement time.
2. During SAS2015 I was told by Dectris that you can set up a threshold per channel. So you could also set 6.4keV and 9keV threshold to adjacent channels and subtract there values. This leads to half the resolution of course.
2.5 Using a semitransparent beam stop made of zinc. Zinc has an absorption edge between 8 and 16keV and reduces the intensity of the 8 and 16keV radiation to similar extend.
Knowing the spectral composition of the radiation may also allow us to compensate for the radiation hardening to determine the true transmission factor, although at high absorptions it would become quite imprecise. Thanks to all the helpful tips received from the readers so far. More ideas are always welcome!
- Never Forget: “Assumption is the mother of all fuck ups“
Comment from Sam Tardif:
“Nice post!
Scanning the threshold sounds good, but how about the change in sensitivity near the channel edges when you change the threshold? Would that impair the quantitative measurement or is it small enough to be negligible?”