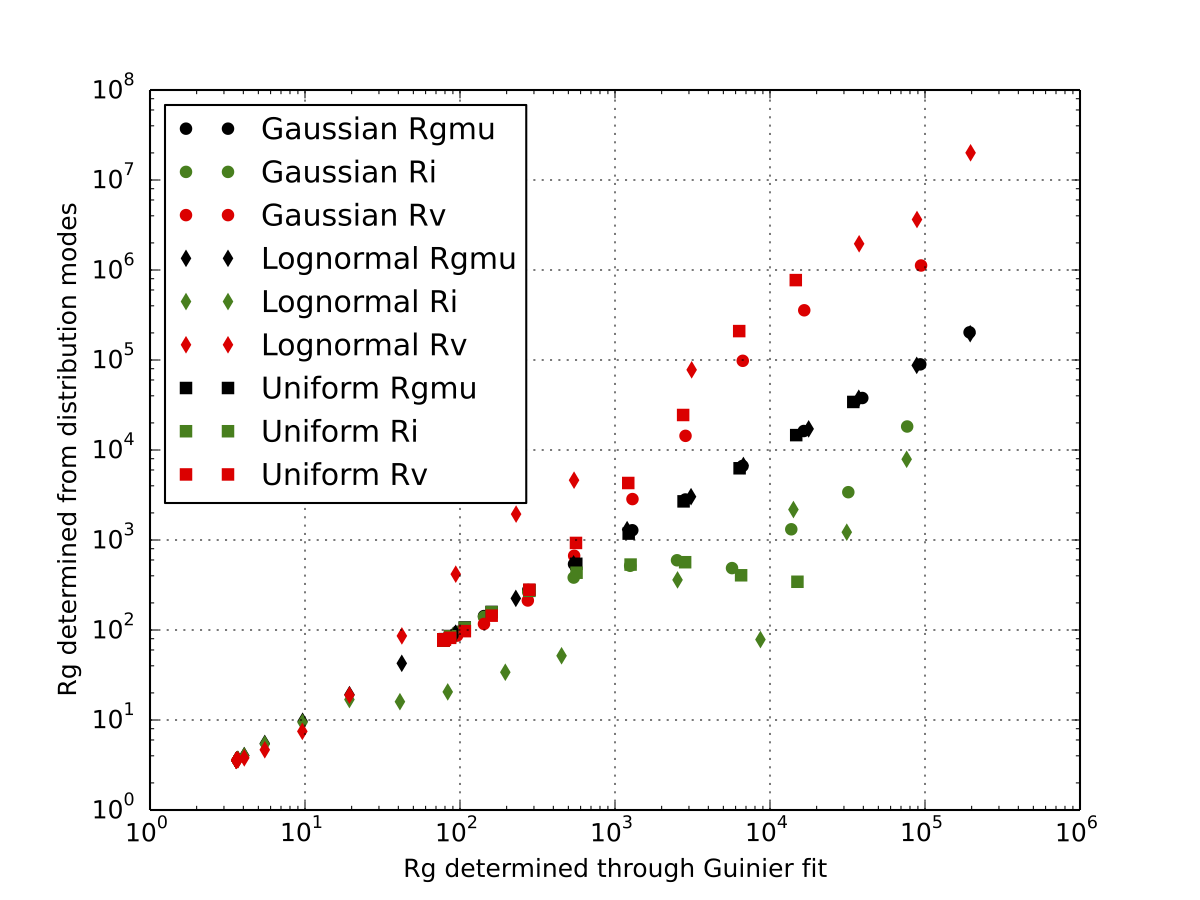
Last week, I was contacted by Christian Gollwitzer (author of this excellent paper) about something posted here (and in particular detailed in this document) a while ago. It concerns the behaviour of the Guinier approxiation for polydisperse systems, and it looks like I made a mistake when writing that document.The document states that the radius of gyration used in the Guinier method for polydisperse systems will be the volume-squared-weighted radius of gyration. However, Christian heard a slightly different message from his colleagues. Time to investigate.
The easiest and most fun way to investigate this is to redo the simulations and fits. It is easy to simulate scattering patterns from polydisperse spheres with a variety of polydispersities, and to then fit these to a particular model to see how well the model works.
For those interested, the derivation and some more background information and references on the true result is jotted down in this document: Guinier_limits_revisited. The Python code used for the simulations and plotting can be downloaded from this link: guinierfit (warning: the code doesn’t look pretty at all!).
In summary, the literature is correct, and the radius of gyration is the square root of that value I derived three years ago: it is the square-root of the volume-squared weighted average radius. However, this is not the same as the volume-weighted or intensity weighted value. Literature references to the correct equation can be found in Otto Glatter’s 1982 book and in (f.ex.) this 2004 paper by Grégory Beaucage. Derivations for Guinier in polyidsperse systems appear to date back to at least 1964, in this paper by R. Baur and V. Gerold.

Leave a Reply