
Contrast variation is commonly used in SANS to highlight a single segment of a mutli-part structure. In SANS it is easy to do this because a wide range of scattering length densities can be accessed by simple mixing of water and deuterated water. In SAXS this is not so easy. A recent arXiv paper [1] by Raul Garcia-Diez, however, shows one method for getting it done in SAXS.
Contrast variation SAXS (CV-SAXS) is typically done by immersion in a (mixture or variety of) solvent(s). For porous structures, contrast variation can be used to study the different types of pores: outside accessible and inaccessible pores. By immersion in a solvent, they can be quantified and dynamics studied [2, 3, 4] (the references happen to be all fibre examples, due to my previous research topic focus…).
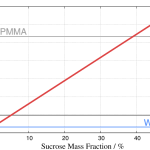
For multi-part structures (core-shell particles, vesicles), CV-SAXS can separate the sizes of the constituent parts. In this case, the structure would be suspended in a series of solvent mixtures with varying scattering length densities (SLDs) (c.f. Garcia-Diez’ paper). As it is tedious and risky to prepare series of accurate solvent mixtures, he chose to use a solvent density gradient with water and sucrose (Figure 0). To be honest, gradients are a very smart way of accessing a wide range of conditions, and I think it is a very good choice here as well.

He creates this by injecting the analyte in a solvent mixture with high SLD at one end of a capillary, and the analyte in a solvent mixture of low SLD on top of that These will slowly mix, and during the mixing process there will be a well-defined SLD gradient from one end of the capillary to the other (with a uniform concentration of analyte). By measuring at various locations along the capillary and along the time-axis, a wide range of SLD contrasts between solvent and analyte are accessed (Figure 1).
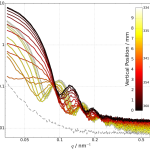
The analysis of CV-SAXS data (Figure 2) is a little more complex because you have a number of datasets of the same structure but with different contrasts. As not much software can deal with this, you are invariably left to write your own fitting method. Let’s hope this will be resolved in the near future, as it is a time-consuming (though instructive) task.
R. Garcia-Diez applied several analysis methods to his data, including a basic Guinier fit and a more elaborate least-squares fitting procedure with classical scattering functions. The least-squares fitting offers a close match to the expected value (and valuable uncertainty estimates). The Guinier method (which needs the polydispersity estimate from the least-squares fit) comes quite close but only after expansion (de-approximation?) of the Guinier approximation to a full sphere scattering function. It is also applied to a smaller range of data, and particularly that data more sensitive to background subtraction issues. Overall, then, the more elaborate least-squares way is the way forward.
The results are very promising indeed, especially given the low contrast in the investigated structures. It is my hope that CV-SAXS can be used alongside ASAXS in the future to get a more consituent-sensitive insight into multi-part structures.
[1] R. Garcia-Diez, C. Gollwitzer, M. Krumrey. Nanoparticle characterization by means of continuous contrast variation in SAXS with a solvent density gradient. arXiv:1409.1776 (2014).
[2] F. Stern. Dependence on moisture content of the small angle X-ray scattering power of cellulose fibres. Trans. Faraday Soc. 51: 430, 1955 DOI: 10.1039/TF9555100430
[3] K. Saijo, O. Arimoto, T. Hashimoto, M. Fukuda, and H. Kawai. Moisture sorption mechanism of aromatic polyamide fibres: diffusion of moisture into regular kevlar as observed by small-angle x-ray scattering technique. Polymer, 35:496–503, 1994.
[4] D. A. Mooney and J. M. D. MacElroy. Differential water sorption studies on kevlar 49 and as-polymerised poly(p-phenylene terephthalamide): adsorption and desorption isotherms. Chemical Engineering Science, 59:2159—2170, Apr 2004.

Leave a Reply