Rebinning is an easy way to reduce the size of your datasets. But does it affect your results?
The effect of (re-)binning your data
(Re-)binning, or averaging, is the practice of reducing the size of a dataset by bunching of datapoints. Of each bunch of datapoints, the mean and standard error on the mean can be determined with higher precision than the original datapoints. The arguments for rebinning are that:
- It reduces the size of your dataset, allowing it to be fit (much) faster
- It can add another estimator for the uncertainty of your data (through analysis of the datapoint spread in a bin)
- A physical binning process is already done by the detector due to the finite pixel size. In rebinning, we effectively redefine the pixel dimensions.
- It allows you to redefine the datapoint intervals, particularly useful for datasets spanning several decades.
So why aren’t we all doing this? There are those among us who are of the opinion that (re-)binning should not be done on data, as it might have unforeseen effects. Time to put a gumshoe on the case and figure out if it has an effect.
The dataset
One practical way to find out if it has an effect is to take a dataset with many datapoints, and fit it within a particular range. We can then rebin the datapoints into fewer bins, and repeat the fit. Any practical effect will have to show up sooner or later due to the binning.
One such dataset is that used in the Round Robin experiment, measured on a synchrotron, and with a suitably large starting number of datapoints (829). The -range of the dataset spans
.
A second dataset a simulation of an extreme case: monodisperse scatterers. While, in practice, monodisperse scatterers are extremely rare, it is the case for which the rebinning should have the most drastic effect. This dataset has been simulated over the same $q$-range as specified above, but for 2000 datapoints in the starting set, with an uncertainty for all datapoints of 1%.
The binning
The rebinning procedure sets a series of bin edges, grouping together the pixels that fall in between two edges. Of this group, the mean is calculated and the uncertainties are propagated through the averaging procedure. If the standard error on the mean (derived from the spread of the datapoint values) is larger than the propagated uncertainty, the uncertainty is reset to assume this larger value.
The evaluation
The evaluation performed is very similar to that employed in the round robin experiment: we are interested in seeing the deviation of the resultant population parameters. By choosing an ever smaller number of bins, we can determine when it deviates.
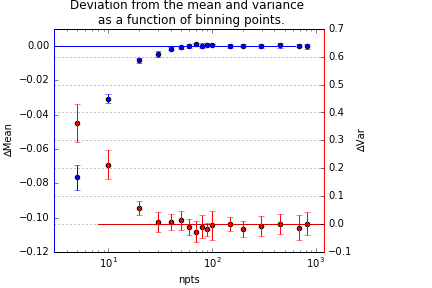
Figure 1 shows the relative deviation of the mean and variance of the distribution, as a function of the number of datapoints. As evident from that graph, meaningful deviations only start appearing when we bin the data to below 40 bins.
For the monodisperse case, however, the situation is drastically different. As you can imagine (and as Figure 2 shows) the rebinning has drastic effects on the variance (so much so that I could not plot it in the original way). Indeed, the variance changes by several orders of magnitude. So at first glance it would seem that for monodisperse scatterers, we should avoid rebinning and measure without any smearing effects in place.
The discussion
Practically, however, this is nonsense. When we translate the variance in the figure above to real units, we have distribution widths orders of magnitude below the size of atoms. Even for the more severe binning variants (i.e. 50 bins), the determined distribution width still remains well shy of an Ångström.
Furthermore, there is no way to avoid any smearing effects in the scattering pattern, which is at the very least limited to the pixel dimensions of your detector, but typically limited to the size and divergence of the beam, and the thickness of the sample. And while you can do desmearing of a scattering pattern in an attempt to retrieve the required features, doing so requires great care and great responsibility (and magnifies your uncertainties).
So while it is ostensibly feasible for (poly-)disperse, but bad for monodisperse patterns to (re-)bin, it makes little difference in reality!

Brian, this is very simplistic example on data with tiny q-range. Rebinning must be done carefully and with consideration to type of sample scattering and data quality. For example, we produce unbinned data sets with around 8500 points spanning over 4 decades in scattering vector (USAXS+SAXS). Such data are very difficult to use for analysis as we generally do not have enough memory/cpu on our desks to do fitting to them. For many polydispersed systems this can be – without loss of information needed for analysis – reduced to 300-400 points. Typically log-q binned for both USAXS and SAXS, but sometimes log-q binned for USAXS and linearly binned for SAXS. On the other hands, for monodispersed systems or systems with diffraction peaks in SAXS (or USAXS) regions the binning has to be done to much larger number of points – 2000 or even 4000 have been used or rare occasions. Proper binning can be done either in data reduction packages or in data analysis packages BUT always with (experienced) human involvement. I actually discuss this during my SAXS analysis courses extensively because this is very important subject… Without a simple, common, solution. So be careful about simplifications as they are quite dangerous.
Dear Jan,
Thank you very much for weighing in on the issue.
So as a rule of thumb, if you have no diffraction peaks or very sharp fringes, can we agree that about 100 bins per decade would be more than sufficient?
Yes, with lack of sharp features and especially on polydispersed systems for sure 100 bins/decade is enough, if not overkill. If the same can be said for monodispersed system where shape reconstruction is going to be attempted (~ protein SAXS) is something expert in different area needs to address.