The FFT is a powerful approach to simulate scattering patterns: feed it a realistic electron density map, and you get an accurate scattering pattern out the other end. Great for simulating the scattering of complex structures, be they hierarchical or with complicated density variations, which can then be used to test whether your analysis approach extracts the relevant morphological parameters with accuracy. It’s got annoying limits, though. Some of these we managed to overcome:
Those who have tried the FFT approach to simulate scattering patterns from realistic electron densities, know that the size of the simulation will be severely restricted due to memory limitations. As the 3D density (and FFT) scale with the third power to the box dimensions in voxels, your normal approach will cease working at about 5123 voxels. That is enough to simulate scattering patterns with a width of about a decade in Q, but not much more than that. Simulating, for example, diffraction peak broadening due to particle- or grain- size limitations, coupled with neighbouring effects alongside the scattering pattern, for example, will not be possible.
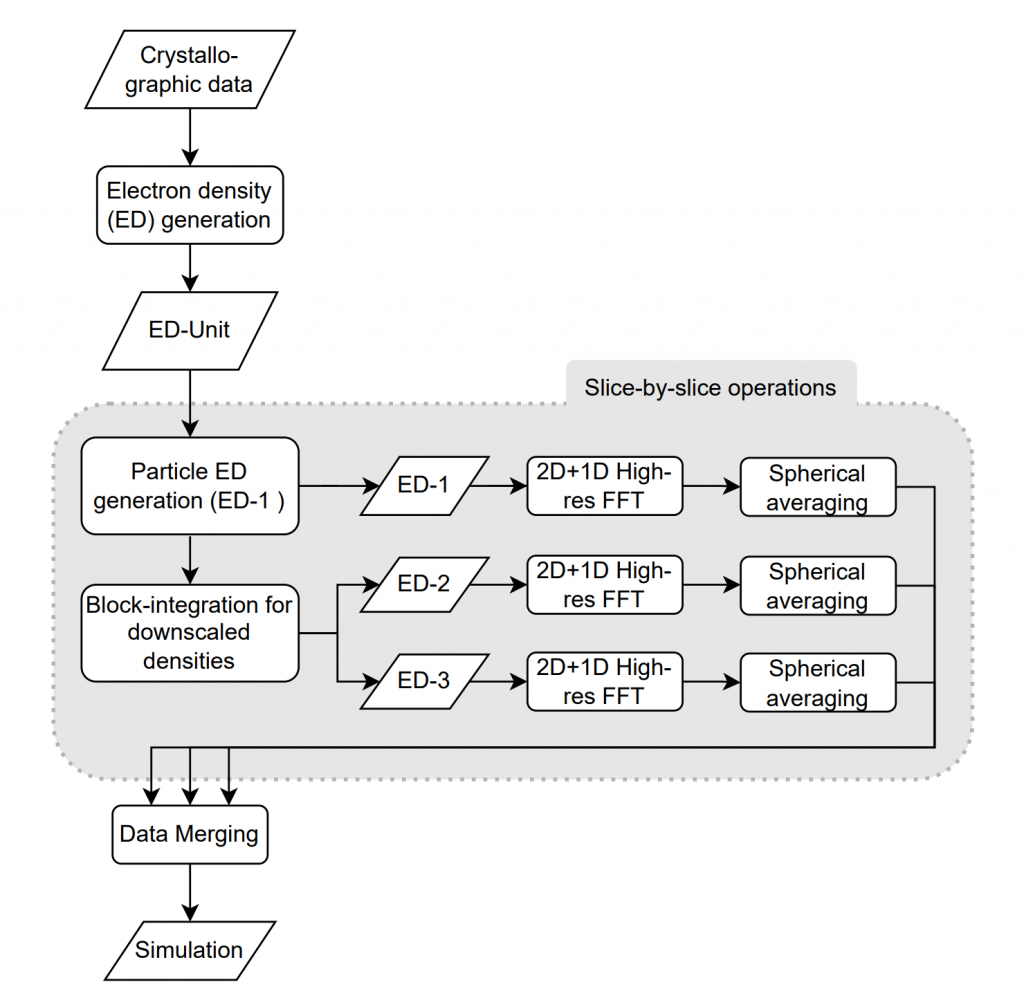
Therefore, I’d asked a master’s student, Sofya Laskina, to pursue an offhand suggestion made by Steen Hansen during my Ph.D. defense. He mentioned it was possible to break apart the 3D FFT and do it in segments. With the help of Sofya, we built a demonstrator to see if we could make that work in practice. With this, we entered a sliced world, where everything had to be sliced up and treated as such, but it turns out to be possible.
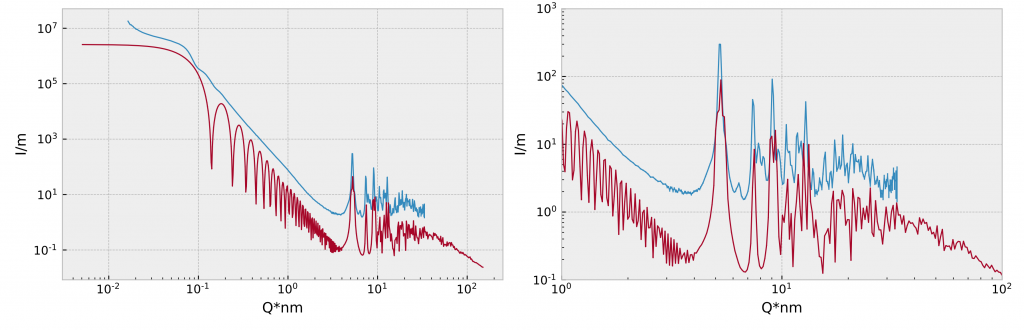
With this approach, we can calculate 3D FFTs on fairly standard PC hardware with box dimensions exceeding 100003 voxels, provided you have sufficient disk space to store the intermediate matrices, and you have a week of time. I’m sure that with a little effort, the code could be sped up by at least an order of magnitude, maybe more.
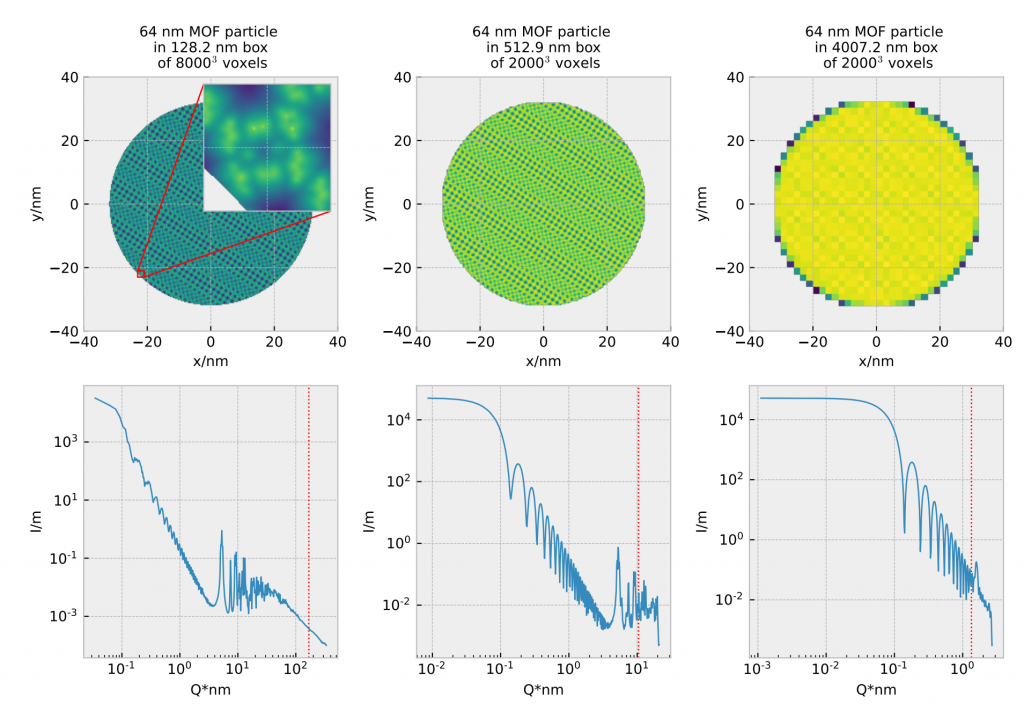
Additionally, we investigated if it’s possible to improve the low-Q behaviour by doing multiple 3D-FFT simulations at different scale levels, and combining them afterwards (Figure 2). This, too, seems to be a practicable approach.
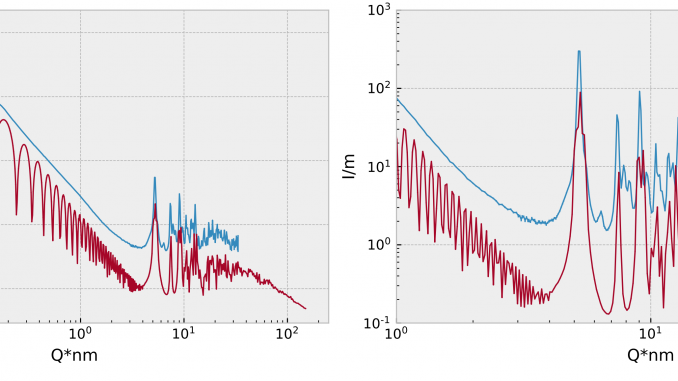
With the help of several others, we were able to demonstrate this approach in our draft manuscript to simulate a monocrystalline MOF particle from the SAXS to WAXS and PDF regions (Figure 1). We’re trying to publish this at the moment.
With the FFTs now sorted, the problem really becomes how to simulate realistic high-resolution electron densities. That is a challenge for which libraries appear to exist that could be used, but they, too, may need modification before they are able to improve the resolution.
If you are interested, however, please do check out the presubmission manuscript here:
[2303.13435] “Ultima Ratio”: Simulating wide-range X-ray scattering and diffraction (arxiv.org)
For those with limited time, and/or those who favor a more visual explanation, there is also a YouTube video available here:
“Ultima Ratio”: Multi-scale, high-resolution 3D-FFT scattering pattern simulations – YouTube
And if you want to see the implementation for yourself, the proof-of-concept jupyter notebook is available on Zenodo:
