Revisiting observability in polydisperse systems: “real” polydispersity

edited on 2011-07-20 14:51 to add equation defining observability

Of course I could not leave you hanging after the last post with that question “does the observability still scale with the radius squared for samples with more than two particles?”. Short answer: yes. Long answer: mostly, with some interesting lessons w.r.t. q-angles and limitations. Click “more” to read on…

I set out to do some more simulations on scattering patterns, this time consisting of a multitude of spherical particles (a thousand or so will do). Initially, I played around with some realistic-looking distributions until I realized that the observability is independent of the distribution. As before, the observability is defined as the maximum fractional contribution of a single particle at a single point in the scattering pattern. So, an observability of 0.2 means that the particle contributes 20% at most to the scattering pattern, at a certain location in q.

 

In this case we are not interested in the absolute observability, which is dependent on the number of particles, but rather on the dependency of the observability with respect to the size of the particles. Last time, it was found that for a two-particle system, the smaller particle will be visible less and less the smaller it gets (due to the volume-square dependency of the intensity of its scattering signal). However, due to the change in the shape of the scattering pattern, the effective reduction in visibility scales with R^(-2). The q at which this is highest turned out to be roughly related to the radius of gyration Rg as q*Rg=2.5. Some approximations were made, the most severe of which was the description of the averaged sphere scattering function using a Universal scattering function equation.

Now, though, due to the large number of particles in our simulation, we can dispense with this approximation and return to the “true” sphere scattering function. Using a uniform size distribution over the range 0<R<1000, for 0.001<q<0.1 the scattering pattern we get are the superposition of the components shown in Figure 1.

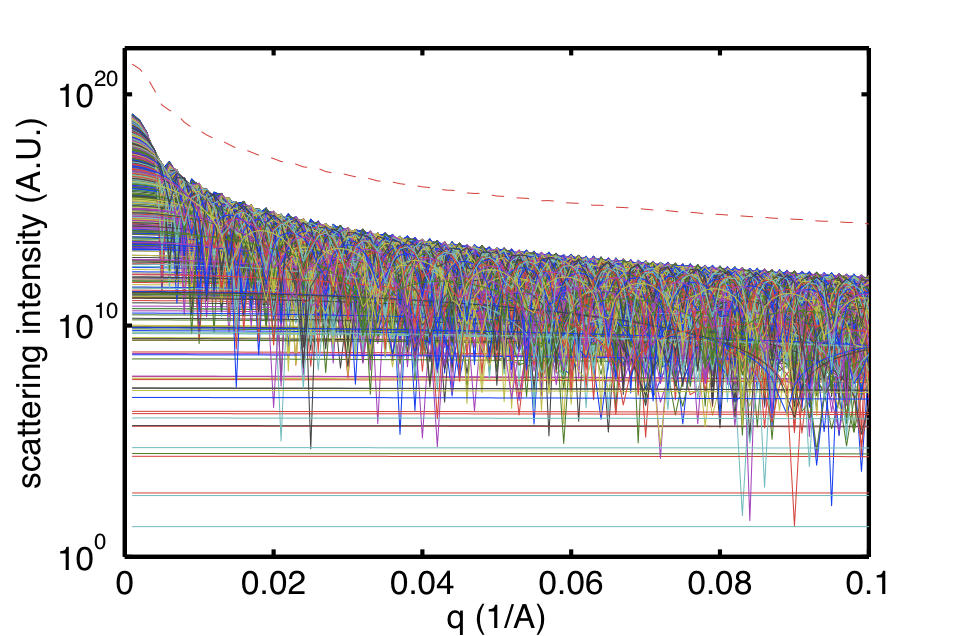
In Figure 1, we see a plethora of contributions overlapping, but also several very flat contributions which almost do not contribute. These are the smallest particles, which we will see later scale with R^(-6) due to the limited q-range.

Plotting the observability and the q at which this observability is largest as a function of the radii in a double-logarithmic plot, Figure 2 results.

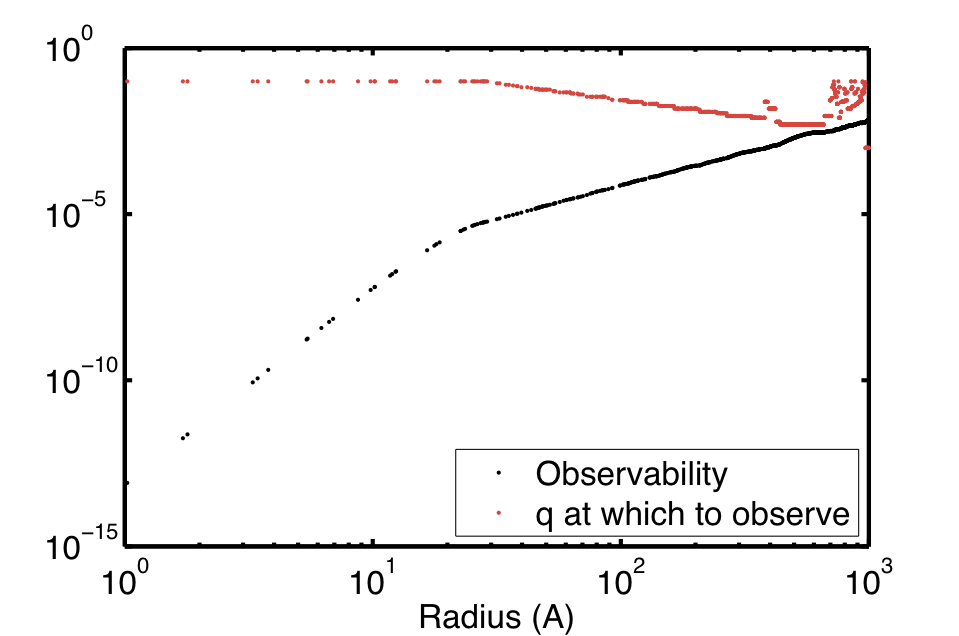
Firstly, the black dots in Figure two follow for the most part an R^(2) relationship of observability. at R<30 however, a gradual transition to an R^(6) relationship is seen. A similar kink is seen in the red dots, where the q at which the observability is largest levels off to our maximum q value, 0.1. At large R, the red dots no longer follow a linear relationship with R (remember the qR=constant relationship mentioned in the previous section?) but oscillates between the maximum q and qR=constant line. Returning to the slopes of the observability, it becomes apparent that the slope of the relationship of the observability versus the radius is related to our maximum measurable q.

Indeed, this “kink”-point can be easily moved by determination of the observability over a different q-range, shown in Figure 3.

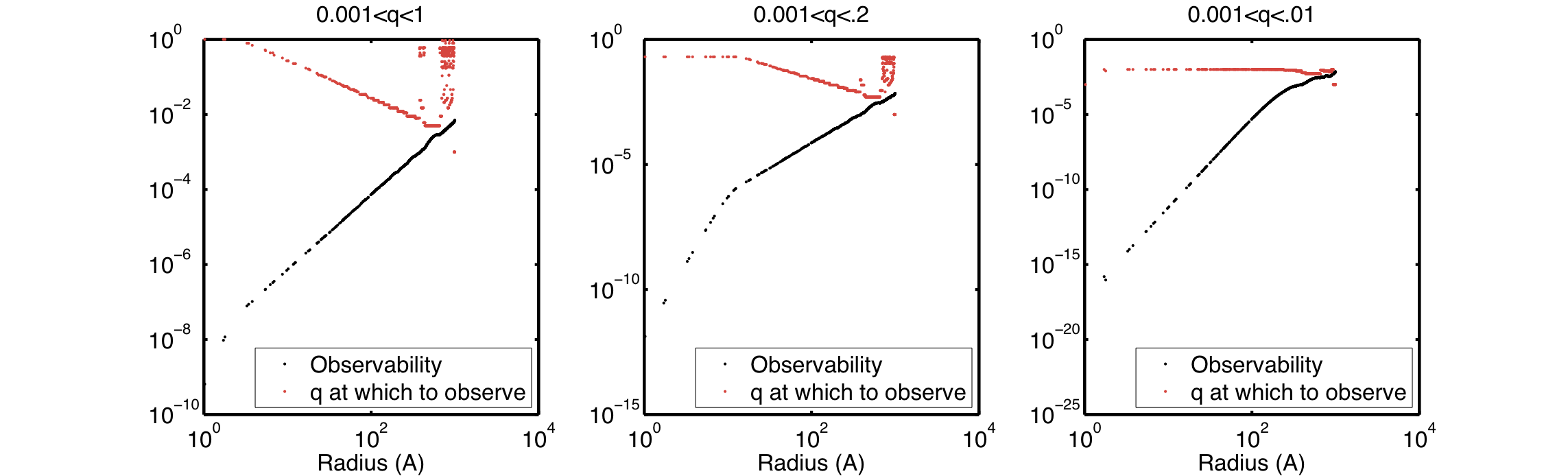
So we see from Figure 3 that the R^(2) slope of the observability is dependent on our maximum q. crossover point is somewhere between R=π/qmax and R=π/(2*qmax). The consequence of this is that if we measure to a certain qmax, the observability of the particles below R=π/qmax scales with R^(6) and these small particles will thus very quickly become invisible (i.e. contributions smaller than the error of the intensity in our scattering patterns). In short: mind your maximum q!

There is an additional thing visible in these plots, which is small “bumps” in observability. We can enhance this by not plotting it on double logarithmic scale, shown in Figure 4.

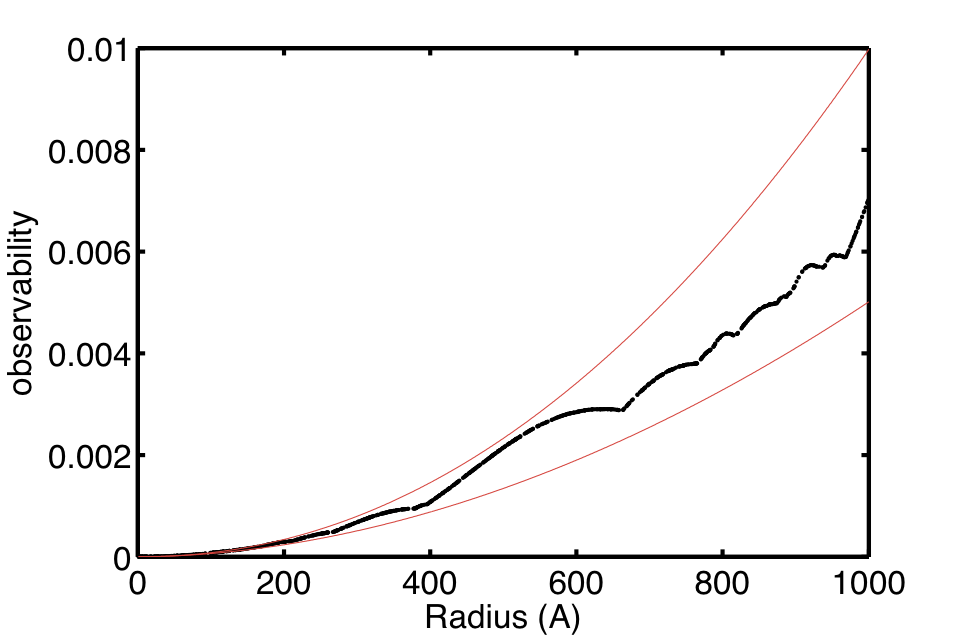
Figure 4 shows us the bumps, which change depending on the step size in q chosen (not shown). They also fall within the power-laws R^(1.9) and R^(2.1), leading me to believe this may be an artefact of some sort. Further investigations will have to be done to reveal the true nature of these.

In conclusion, then, the observability of spherical particles in polydisperse systems scales roughly with the radius squared, with the side-note that R should be bigger than π/qmax for this to be true. Below this radius, the scaling trends quickly towards R^6 (true volume-squared scaling), rendering those particles rapidly invisible to small-angle scattering techniques.