Does it matter part 6.1: The effect of finite width pixels

This short investigation was prompted by the instrument here at BAM and the associated Anton Paar software. The software determines the beam center behind the transparent beamstop, apparently based on a polynomial fit through (just) four datapoints. This means that the beam center can vary a bit from measurement to measurement, typically on the order of fractions of a pixel.

We then set out to quantify just how much that, as well as the finite pixel width, would affect our size determination. Here is a back-of-the-envelope calculation…

Introduction

The finite pixel size gives us a pixel width in which can affect the resolution of the smallest angles. This may have an effect on the accuracy of the sizes determined on this instrument. Similarly, variation in the sub-pixel beam center determination may also affect this accuracy.

It should be a simple geometric calculation to find out by how much this affects our measurements.

Geometric data

We are using a Kratky camera with a sample-to-detector distance of 0.307 m. The pixel size on the Dectris Mythen detector attached to it is 50 m. The radiation is Copper k and k radiation, whose mixture gives us an weighted apparent wavelength of 0.1542(2) nm. When we assume perpendicularity of the detector with the point of normal incidence at the beam center, the nm. The useful data (peeking over the beamstop) starts at nm.

Approach

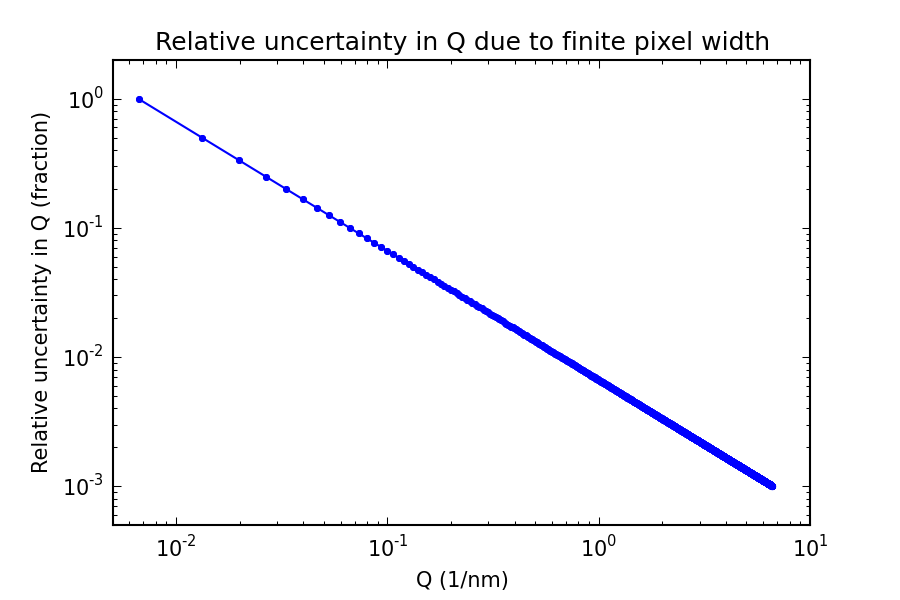
The relative uncertainty due to one pixel width in Q for the first 1000 pixels is shown in Figure 1. This shows that after ten pixels, the uncertainty in Q has reduced to 10% (which makes sense given what has been plotted here).

 

So far, so straightforward. So how does this translate into uncertainty in the size determination? The approximation of has been working reasonably well in my experience, so using that, we can get an estimate on the uncertainty in size. For somewhat polydisperse systems, indicates the location of the transition to the Porod slope.

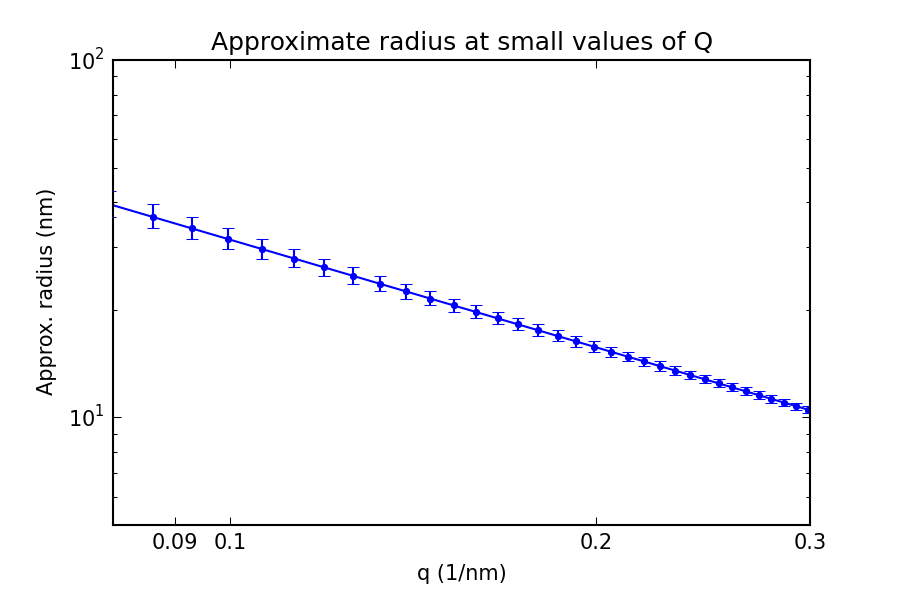
We may estimate lower and upper limits of the deviation by using:
and (c.f. Figure 2). This data in Figure 2 has been clipped from the onset of the useful data range (), to a few datapoints above that. Not much to see here, since the error bars on the approximate radius are relatively small.

The relative uncertainty on the radius for this instrument configuration can perhaps shed a little bit more light on the situation. This representation (Figure 3) is quite elucidating, showing a large uncertainty in size determination, solely due to the pixel width! You can see the problem reflected in the datapoint spacing: for large sizes, there are only a few datapoints available. In effect, for large sizes the uncertainty in size determination will approach several nm.

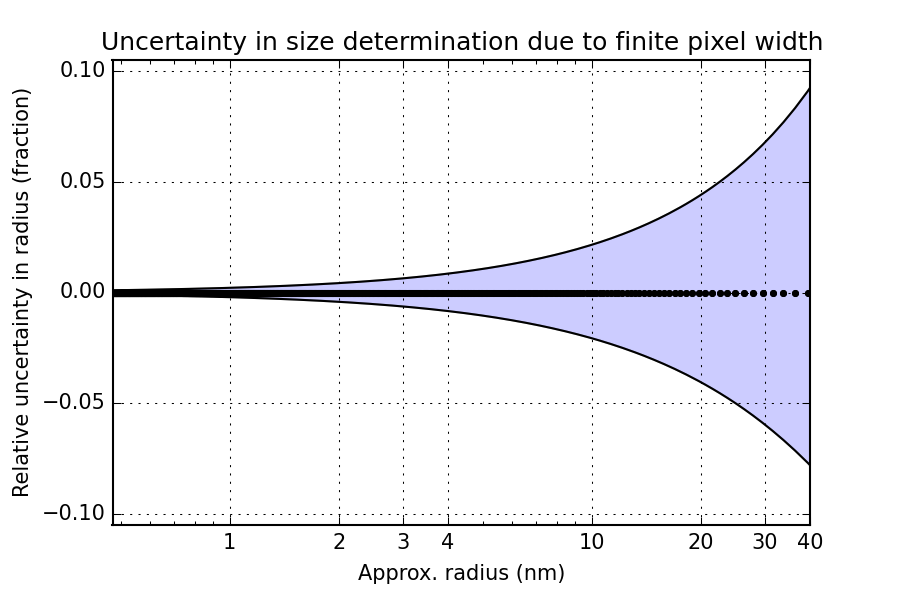
Note, that this does not even take the beam size on the detector into account, which would also add to the uncertainty. For the Kratky-type instruments, the beam width is typically 50-100 micrometer, but for standard pinhole-collimated instruments it may be much bigger. I would strongly recommend those using pinhole-collimated instruments to do this straightforward derivation for themselves so you can add a weight to your estimates.

Disclaimer

Now it should be stressed that this is only an estimate, and a more thorough derivation may be necessary to quantify the actual practical accuracy limits of the technique.

However, if you have a polydisperse system you cannot benefit from fringes in the patterns to increase your accuracy. In that case, this approximation is quite indicative, and thus the uncertainties from geometric considerations alone will give you this result.