Weighted binning

Hello,

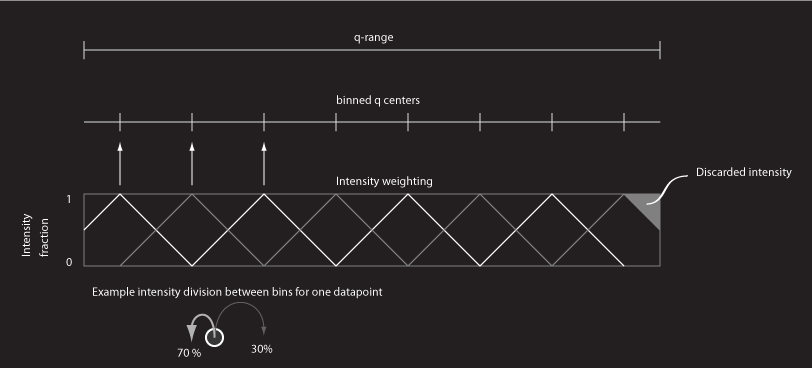
Once again, I’d like to present a binning routine. This time it’s a weighted binning routine, which instead of simply summing all intensity in one bin of a certain width, it splits the intensity to neighbouring bins based on their proximity to the bin centres:

As is explained in the graphics, this implies that there is a loss of intensity required in order to keep the first and last bin in line with the other bins. The advantage of this binning function, however, is that it should result in a smooth binned curve with no moire-like effects.

Speedwise, it bins a 2048×2048 image in about 7 seconds on a 2.4 GHz Intel core 2 duo processor (single core), which is just as quick as the equal intensity binning routine discussed in a previous post. As always, if you have any suggestions or improvements, please let me know so I can update the code.

The code itself can be found here: binning_weighted code

It is also given below (behind the “more” button). Leave comments please!

function [qbin,Ibin]=binning_weighted(q,I,nbins)
%this function implements binning of intensity into bins. The intensity is
%divided between the bin centers depending on their distance to the center.
%This may cause the first and last bin to be filled inequally with
%intensity, so be careful when using those. Some intensity has to be
%discarded to alleviate this issue.

%reshape q and I to x by 1 vector
q=reshape(q,size(q,1)*size(q,2),1);
I=reshape(I,size(I,1)*size(I,2),1);
qmin=min(q);
qmax=max(q);
stepsize=(qmax-qmin)/nbins;
%bin center positions
binc=qmin+0.5*stepsize:stepsize:qmax-0.5*stepsize;
%sort q,I to q
[qsort,qsorti]=sort(q);
Isort=I(qsorti);
%first implementation: using a loop function
Ibin=zeros(size(binc));
for bini=1:length(binc)

 %first optimisation: only calculate the values that actually matter;
 %success, these two find's reduce the calculation time from 57 seconds
 %to 7 seconds. The region before the loop takes 1 second, so further
 %optimisations will have to occur within the loop.
 qi(1)=find(qsort>(binc(bini)-stepsize),1,'first'); 

 qi(2)=find(qsort<(binc(bini)+stepsize),1,'last');

 %compute distances 

 qdist=abs(qsort(qi(1):qi(2))-binc(bini)); 

 %compute the weighting factors 

 weightfact=(qdist<stepsize).*(1-qdist./stepsize); 

 %sum the intensities in one bin 

 Ibin(bini)=sum(Isort(qi(1):qi(2)).*weightfact);
end
qbin=binc;